Ruch jednostanie zmienny to ruch, w którym prędkość zmienia się w sposób jednostajny czyli rośnie lub maleje o stałą wartość w jednostce czasu. Do ruchów zmiennych zaliczamy jednostajnie przyspieszony (np. spadające z drzewa jabłko) i ruch jednostajnie opóźniony (np. podrzucona pionowo do góry piłka). Przyspieszenie w tym ruchu ma stałą wartość.
Korzystając z definicji przyspieszenia możemy wyprowadzić wzór na prędkość końcową:
$latex a = \frac{\Delta V}{\Delta t} = \frac{V_k – V_p}{\Delta t}$
$latex V_k = V_p + a \cdot t \:\:\: $ [równanie ruchu #1]
Dlaczego we wzorze na prędkość końcową pojawiło się t? Zauważmy, że $latex \Delta t = t-t_p$ ale ponieważ $latex t_p = 0$ to $latex \Delta t = t$
Ponieważ w ruchu jednostajnym przyspieszenia jest stałe to prędkość średnia będzie równa dokładnie połowie różnicy pomiędzy prędkością końcową a początkową.
$latex V_{śr} = \frac{V_k – V_p}{2} \:\:\: $ [równanie ruchu #2]
Mając prędkość średnią (równanie #2) drogę możemy policzyć mnożąc prędkość średnia przez czas trwania ruchu.
$latex s = V_{śr} \cdot t $
$latex s = \frac{V_k – V_p}{2} t $
Podstawiając Vk z równania ruchu #1 przekształcamy i otrzymujemy:
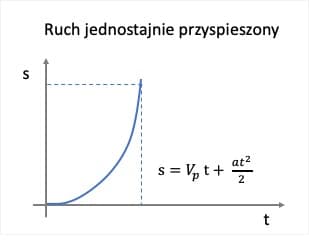
$latex s = V_p \cdot t + \frac{a \dot t^2}{2} \:\:\:$ [równanie ruchu #3]
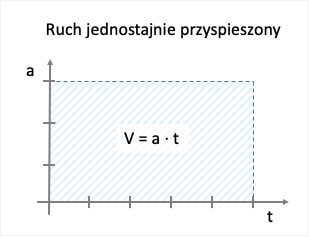
Przeanalizujmy teraz te same zależności na wykresach. Przyspieszenie w ruchu jednostajnie zmiennym ma stałą wartość w czasie. Pole prostokąta pod wykresem zależności przyspieszenia od czasu odpowiada prędkości uzyskanej w czasie t.
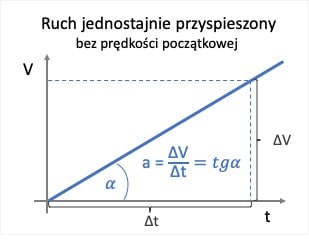
W ruchu jednostajnie przyspieszonym prędkość rośnie liniowo o stałą wartość w czasie – jest to przyspieszenie. Im większa wartość przyspieszenia tym większe nachylenie prostej prędkości. Nachylenie prostej czyli w tym przypadku przyspieszenie możemy opisać matematycznie jako stosunek zmiany wartości na osi Y (w tym przypadku V) to zmiany wartości na osi X (w tym przypadku t) dla dwóch dowolnych punktów prostej.
W trygonometrii ten stosunek nazywany jest tangensem. Nachylenie krzywej jest równe wartości jej pochodnej. Przyspieszenie zależy od zmiany prędkości w czasie – jest jej pochodną.
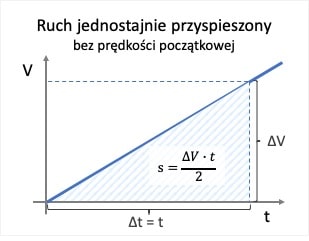
W ruchu jednostajnie przyspieszonym bez prędkości początkowej pole trójkąta pod wykresem zależności prędkości od czasu odpowiada przebytej drodze.
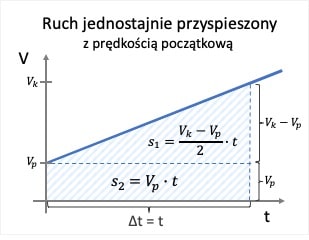
W ruchu jednostajnie przyspieszonym z prędkością początkową na wykresie zależności prędkości od czasu droga będzie sumą pól kwadratu oraz trójkąta.
W ruchu jednostajnie przyspieszonym zależność drogi od czasu jest funkcją kwadratowa – jej wykresem jest parabola.