Korzystając z huśtawki na pewno zauważyliście, że na huśtawce najszybciej poruszamy się w punkcie najniższym (punkcie równowagi) a w punktach największego wychylenia, gdy znajdujemy się najwyżej na chwilę zatrzymujemy się. W tym ruchu drgającym energia potencjalna grawitacji (która zależy od wysokości) zamienia się na energię kinetyczną (która zależy od prędkości) i na odwrót. Suma tych energii pozostanie stała, jeżeli pominiemy straty energii np. na pokonanie oporów ruchu.

1. Energia w ruchu huśtawki

Ruch huśtawki podobnie jak ruch wahadła to przykład ruchu drgającego.

• W położeniu równowagi energia kinetyczna rozpędzonej huśtawki będzie największa (zależy ona od prędkości). Zmiana energii potencjalnej grawitacji (która zależy od wysokości) wyniesie zero względem punktu odniesienia na tej samej wysokości
• W położeniach największego wychylenia czyli amplitudy energia kinetyczna huśtawki wyniesie zero (zależy ona od prędkości a w tych punktach huśtawka się zatrzymuje na chwile przed zmianą kierunku). W tych punktach zmiana energii potencjalnej grawitacji (która zależy od wysokości) będzie największa względem położenia równowagi.

Jeżeli zaniedbamy opory ruchu to suma energii potencjalnej grawitacji oraz energii kinetycznej czyli całkowita energia mechaniczna układu huśtawki pozostanie stała i równa pracy włożonej na wychylenie z położenia równowagi. Huśtawka pozostanie w ruchu zmieniając jeden rodzaj energii w drugą.

	Zmiana energii potencjalnej grawitacji	Energia kinetyczna	Suma energii
Położenie równowagi	Zero – względem tej wysokości	Największa w ruchu	Stała, pomijając straty
Położenie największego wychylenia	Największa – względem położenia równowagi	Zero	Stała, pomijając straty

Czy huśtawka rzeczywiście może ciągle pozostać w ruchu? Z obserwacji oraz zasady zachowania energii wiemy, że w końcu się zatrzyma spowolniona przez opory ruchu takie jak opór powietrza oraz tarcie metalowych elementów. Wykonując dodatkową pracę np. popychając huśtawkę czy wychylając się możemy te straty energii uzupełniać i kontynuować zabawę.

Zadanie

Które zdania opisujące przemiany energii w ruchu drgającym są prawdziwe?

a) Energia kinetyczna wahadła jest najmniejsza w położeniu równowagi
b) Energia potencjalna jest najmniejsza w położeniu największego wychylenia
c) Suma energii potencjalnej i kinetycznej jest stała, jeżeli pominiemy opory ruchu

Odpowiedź: c

Wskazówki: Wahadło (tak jak dziecko na huśtawce) największą prędkość rozwija przechodząc przez położenie równowagi, energia kinetyczna ciała zależy od kwadratu jego prędkości. Im prędkość większa tym energia kinetyczna większa. W położeniu największego wychylenia ciało na chwile zatrzyma się, ale będzie znajdować się najwyżej a więc jego energia potencjalna będzie najwyższa. Podczas ruchu energia potencjalna będzie zamieniać się na kinetyczną a kinetyczna na potencjalną. Jeżeli zaniedbamy opory ruchu to ich suma pozostanie stała.

2. Energia w ruchu wózka na sprężynie

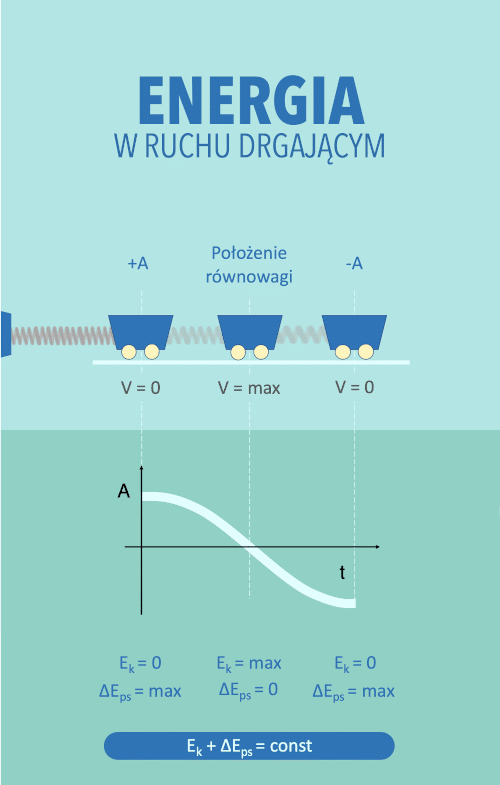
W ruchu drgającym z wykorzystaniem sprężyny energia potencjalna sprężystości będzie zamieniła się na energię kinetyczną i na odwrót. Wyobraźmy sobie wózek zaczepiony na ściśniętej sprężynie do ściany, przy zaniedbywalnych oporach ruchu.

• W położeniu równowagi energia kinetyczna rozpędzonego wózka będzie największa (zależy ona od prędkości). W tym położeniu sprężyna się całkowicie rozciągnie i energia potencjalna sprężystości będzie równa zero.
• W położeniach największego wychylenia wózek na chwile zatrzyma się przed zmianą kierunku ruch i jego energia kinetyczna wyniesie zero (zależy ona od prędkości). W tych punktach sprężyna będzie najbardziej odkształcona a jej energia potencjalna sprężystości (która zależy od odkształcenia) będzie największa.

Jeżeli zaniedbamy opory ruchu to suma energii potencjalnej sprężystości oraz energii kinetycznej czyli całkowita energia mechaniczna układu wózka pozostanie stała i równa pracy włożonej na wychylenie z położenia równowagi. Wózek pozostanie w ruchu zmieniając jeden rodzaj energii w drugą.

---

PRZYDATNY ARTYKUŁ? Udostępnij link innym:

Pozostałe tematy z działu: RUCH DRGAJĄCY I FALOWY

Ruch drgający – amplituda, okres drgań, częstotliwość | Ruch okresowy wahadła | Ruch ciężarka na sprężynie | Przemiany energii w ruchu drgającym | Wykresy ruchu drgającego | Czym jest fala? | Fale mechaniczne | Fale dźwiękowe: infradźwięki, dźwięki słyszalne, ultradźwięki | Fale elektromagnetyczne | Przykładowe zadania z ruchu drgającego i falowego | Komplet testów na sprawdzian