Ze zjawiskiem ruchu stykamy się na co dzień – obserwując pędzące samochody, wyrzucając papierek do kosza czy też podziwiając krążący dookoła Ziemi księżyc.

Kinematyka to dział fizyki zajmujący się badaniem, w jaki sposób poruszają się obiekty. Kinematyka, razem z dynamiką, która opisuje przyczynę ruchu czyli siły, należą do dziedziny zwanej mechaniką.

Zagadnienia kinematyki w szkole średniej:

• Układ odniesienia i względność ruchu
• Pojęcia: ruch, położenie, tor, droga
• Ruch i jego wielkości wektorowe: przemieszczenie, prędkość, przyspieszenie
• Klasyfikacja ruchów ze względu na tor i zmianę prędkości
• Ruch jednostajny prostoliniowy
• Ruch jednostajnie przyspieszony prostoliniowy
• Swobodne spadanie
• Rzuty: rzut pionowy, rzut poziomy, rzut ukośny (poziom rozszerzony)
• Ruch jednostajny po okręgu: okres, częstotliwość, prędkość liniowa, przemieszenie kątowe, prędkość kątowa, przyspieszenie dośrodkowe, przyspieszenie kątowe, przyspieszenie styczne
• Ruch niejednostajny po okręgu (poziom rozszerzony)

Dzień dobry. Nazywam się Leszek Bober. Od 35 lat zajmuję się nauczaniem fizyki i jest to moja wielka pasja. Zapraszam Cię serdecznie do lektury tego artykułu oraz do korzystania z innych moich materiałów.

1. Układ odniesienia i względność ruchu

Czy podróżując pociągiem lub samolotem jesteśmy w ruchu? I tak i nie. Tak, względem ziemi. Natomiast nie, względem tych maszyn (i dlatego w miarę spokojnie możemy podczas takich podróży wypić herbatę).

Ruch jest pojęciem względnym. Ciało może znajdować się względem jednego układu odniesienia w ruchu, a względem drugiego w spoczynku.

Układem odniesienia nazywamy ciało, względem którego określamy położenie innych ciał.

2. Podstawowe pojęcia kinematyki

Ruch: Ciało porusza się, jeżeli zmienia swoje położenie względem układu odniesienia (innego ciała) w czasie.

Położenie: Położenie ciała to punkt, w którym się ono znajduje. Położenie ciała określamy, podając jego współrzędne (na osi liczbowej, wykresie lub mapie). Do opisania ruchu po prostej potrzebujemy jednej współrzędnej x. Do opisania ruchu w dwóch wymiarach np. na płaszczyźnie potrzebujemy dwóch współrzędnych (x, y). Do opisania ruchu w przestrzeni potrzebujemy trzech współrzędnych (x, y, z)

Tor: Torem nazywamy krzywą, po której porusza się ciało. Ruchy możemy podzielić na podstawie kształtu ich toru. Ruch po lini prostej nazywamy ruchem prostoliniowym. Ruch po lini krzywej nazywamy krzywoliniowym. Przykładami ruchów krzywoliniowych są ruchy po okręgu i rzuty poziome.

Droga: Droga jest to długość odcinka toru między dwoma wybranymi położeniami.

3. Wielkości wektorowe ruchu

Dokonując pomiarów ruchu często mówimy o przemieszczeniu, prędkości i przyspieszeniu. Są to wielkości wektorowe czyli takie, które posiadają wartość oraz kierunek.

3.1. Przemieszczenie

Przemieszczenie (wektor przesunięcia) jest to wektor o początku w punkcie odpowiadającym położeniu początkowemu ciała, i końcu w punkcie odpowiadającym położeniu końcowemu ciała.

Przykład przemieszenia: turysta przemierzył 5 km w kierunku zachodnim po czym zawrócił i przeszedł jeszcze 2 km w kierunku wschodnim. Pomimo, że łącznie pokonał 7 km to jego przemieszczenie to 3 km a kierunek to zachód – w takiej odległości od punktu wyjścia i w takim kierunku względem punktu wyjścia znajdował się na koniec swojej wędrówki

3.2. Prędkość i szybkość

W języku polskim, potocznie prędkość i szybkość używane są zamiennie. W fizyce, jeżeli chcemy wyrazić się precyzyjnie niekiedy te pojęcia rozróżniamy. Prędkość jest wielkością wektorową czyli posiada wartość i kierunek np. samochód poruszał się z prędkością 120 km/h na północ. Wartość prędkości nazywana czasem szybkością jest wielkością skalarną i posiada tylko wartość np. 60 km/h.

Prędkość to wielkość wektorowa, opisująca jak szybko ciało przemieszcza się względem układu odniesienia. Prędkość średnią obliczmy dzieląc długość wektora przesunięcia (przemieszczenie) przez czas, w którym to przemieszczenie nastąpiło.

\large V_{śr} = \frac{przemieszczenie}{czas\:przemieszczenia} \large V_{śr} = \frac{pozycja\:końcowa\:-\:pozycja\:początkowa}{czas\:przemieszczenia}

Stosunek drogi do czasu potrzebnego na jej pokonanie bywa nazywany szybkością lub wartością prędkości. .

\large szybkość\:średnia = \frac{droga}{czas}

Dla ruchu w jednym kierunku wartości prędkości i szybkości bedą takie same ale w pozostałych przypadkach mogą się różnić.

Przykład: Oblicz prędkość oraz szybkość średnią turysty, który przemierzył 5 km w kierunku zachodnim a następnie zawrócił i przeszedł jeszcze 2 km w kierunku wschodnim w czasie 1,4 godziny.

szybkość\:średnia = \frac{droga}{czas} szybkość\:średnia = \frac{7km}{1,4h} = 5\:km/h prędkość\:średnia = \frac{przemieszczenie}{czas} prędkość\:średnia = \frac{5km - 2km}{1,4\:h} = ~2,14\:km/h

Prędkość chwilowa to prędkość, z którą ciało porusza się w danej chwili. To właśnie prędkość chwilową pokazuje prędkościomierz w samochodzie. Możemy też powiedzieć, że w ujęciu matematycznym prędkość chwilowa to prędkość średnia dla nieskończenie krótkiego przedziału czasu. Prędkość chwilowa będzie równa co do wartości szybkości bo dla nieskończenie krótkiego czasu przesunięcie będzie równe drodze.

Prędkość opisuje jak szybko zmienia się położenie, a więc jest jego pochodną. Jej wartość jest równa nachyleniu prostej stycznej do wykresu położenia od czasu.

3.3. Przyspieszenie

Przyspieszenie pokazuje nam jak szybko zmienia się prędkość np. jak dynamicznie może przyspieszyć samochód.

Wartość przyspieszenia średniego możemy obliczyć dzieląc zmianę prędkości przez czas, w którym ta zmiana nastąpiła:

\large a = \frac{\Delta  V}{\Delta t} = \frac{(V_k - V_p)}{\Delta t}

\large a – przyspieszenie
\large \Delta V – zmiana prędkości
\large V_k – prędkość końcowa
\large V_p – prędkość początkowa
\large \Delta t – czas, w którym nastąpiła zmiana prędkości

Przyspieszenie chwilowe to przyspieszenie, z którą ciało porusza się w danej chwili. Możemy powiedzieć, że w ujęciu matematycznym przyspieszenie chwilowe to przyspieszenie średnie dla nieskończenie krótkiego przedziału czasu.

Przyspieszenie opisuje jak szybko zmienia się prędkość, a więc jest jego pochodną (i drugą pochodna drogi). Wartość przyspieszenia jest równa nachyleniu prostej stycznej do wykresu prędkości od czasu.

4. Klasyfikacja ruchów

Ruchy możemy podzielić ze względu na tor, po którym porusza się ciało oraz ze względu na zmiany prędkości ciała.

Podział ruchów ze względu na tor:

• Ruch prostoliniowy – ruch odbywający się po lini prostej czyli w jednym wymiarze np. pociąg metra czy samochód, który porusza się w lini prostej.
• Ruch krzywoliniowy – ruch odbywający się po krzywej w dwóch lub trzech wymiarach tak jak w ruchu po okręgu (np. dziecko korzystające z karuzeli) lub rzucie poziomym (np. kamyk rzucony przed siebie)

Podział ruchów ze względu na zmianę prędkości:

• Ruch jednostajny – ruch ze stałą (czyli jednostajną) prędkością
• Ruch zmienny – ruch ze zmieniającą się prędkością
  • Ruch jednostajnie zmienny – ruch, w którym prędkość zmienia się w sposób jednostajny czyli rośnie lub maleje o stałą wartość w jednostce czasu. Do ruchów zmiennych zaliczamy jednostajnie przyspieszony (np. spadające z drzewa jabłko) i ruch jednostajnie opóźniony (np. podrzucona pionowo do góry piłka)
  • Ruch niejednostajnie zmienny – ruch, w którym prędkość ciała zmienia się w sposób niejednostajny (nieregularny) np. samochód podczas rajdu terenowego

5. Ruch jednostajny prostoliniowy

Ruch jednostajny prostoliniowy to taki ruch, którego torem jest linia prosta a prędkość ciała jest stała np. ruch pociągu lub samochodu poruszających się ze stałą prędkością po lini prostej.

W ruchu jednostajnym prostoliniowym ciało w jednakowych odcinkach czasu przebywa jednakową drogę. Droga ta jest proporcjonalna do czasu trwania ruchu. Na przykład jeżeli samochód porusza się ruchem jednostajnym prostoliniowym z prędkością 10 m/s to w czasie 1 sekundy pokona 10 metrów, w ciągu 2 sekund 20 metrów i każdej następnej podobnie.

W ruchu prostoliniowym, zwrot prędkości nie zmienia się a długość wektora przesunięcia jest równa przebytej drodze. Wartość prędkości (szybkość) można wtedy obliczyć dzieląc drogę przez czas, w którym ta droga została przebyta.

\large V = \frac{s}{t}

\large V – prędkość
\large s – droga
\large t – czas

Jednostką prędkości jest 1 m/s. Ciało porusza się z prędkością 1 m/s, jeżeli  drogę 1 metra przebędzie w ciągu 1 sekundy.

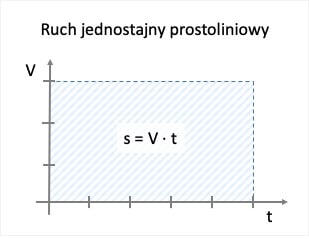
Prędkość w ruchu jednostajnym, prostoliniowym nie zmienia się. Wykresem zależności prędkości od czasu dla ruchu jednostajnego jest prosta równoległa do osi czasu. Wyliczając ze wzoru na prędkość drogę otrzymujemy s = V ⋅ t. Tym samym wzorem możemy wyrazić pole prostokąta pod wykresem zależności prędkości od czasu a zatem odpowiada ono właśnie przebytej drodze.

Wykres zależności drogi od czasu dla ruchu jednostajnego prostoliniowego to linia prosta o nachyleniu odpowiadającym prędkości ciała będącego w ruchu. Im większa prędkość ciała tym większe będzie nachylenie prostej (bardziej stroma będzie prosta).

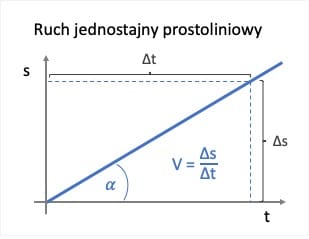
Zauważmy, że wykres ten przedstawia funkcję liniową: s = V ⋅ t. Dla funkcji liniowej nachylenie jest określone przez współczynnik kierunkowy prostej – w tym przypadku V.

Nachylenie prostej czyli prędkość możemy opisać matematycznie jako stosunek zmiany wartości na osi Y (w tym przypadku s) to zmiany wartości na osi X ( w tym przypadku t) dla dwóch dowolnych punktów prostej.

\large V = \frac{\Delta s}{\Delta t}

W trygonometrii ten stosunek nazywany jest tangensem. Nachylenie krzywej jest równe wartości jej pochodnej. Prędkość zależy od zmiany drogi w czasie – jest pochodną.

6. Ruch jednostajnie zmienny (przyspieszony lub opóźniony)

Ruch jednostanie zmienny to ruch, w którym prędkość zmienia się w sposób jednostajny czyli rośnie lub maleje o stałą wartość w jednostce czasu. Do ruchów zmiennych zaliczamy jednostajnie przyspieszony (np. spadające z drzewa jabłko) i ruch jednostajnie opóźniony (np. podrzucona pionowo do góry piłka). Przyspieszenie w tym ruchu ma stałą wartość.

Korzystając z definicji przyspieszenia możemy wyprowadzić wzór na prędkość końcową:

\large a = \frac{\Delta  V}{\Delta t} = \frac{V_k - V_p}{\Delta t}

\large V_k = V_p + a \cdot t \:\:\: [równanie ruchu #1]

Dlaczego we wzorze na prędkość końcową pojawiło się t? Zauważmy, że \Delta t = t-t_p ale ponieważ t_p = 0 to \Delta t = t

Ponieważ w ruchu jednostajnym przyspieszenia jest stałe to prędkość średnia będzie równa dokładnie połowie różnicy pomiędzy prędkością końcową a początkową.

\large V_{śr} = \frac{V_k - V_p}{2} \:\:\: [równanie ruchu #2]

Mając prędkość średnią (równanie #2) drogę możemy policzyć mnożąc prędkość średnia przez czas trwania ruchu.

\large s = V_{śr} \cdot t \large s = \frac{V_k - V_p}{2} t

Podstawiając Vk z równania ruchu #1 przekształcamy i otrzymujemy:

\large s = V_p \cdot t + \frac{a \dot t^2}{2} \:\:\: [równanie ruchu #3]

Przeanalizujmy teraz te same zależności na wykresach. Przyspieszenie w ruchu jednostajnie zmiennym ma stałą wartość w czasie. Pole prostokąta pod wykresem zależności przyspieszenia od czasu odpowiada prędkości uzyskanej w czasie t.

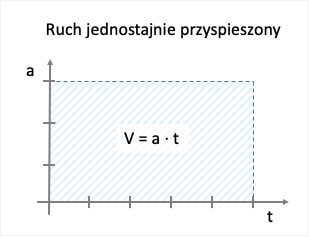
W ruchu jednostajnie przyspieszonym prędkość rośnie liniowo o stałą wartość w czasie – jest to przyspieszenie. Im większa wartość przyspieszenia tym większe nachylenie prostej prędkości. Nachylenie prostej czyli w tym przypadku przyspieszenie możemy opisać matematycznie jako stosunek zmiany wartości na osi Y (w tym przypadku V) to zmiany wartości na osi X (w tym przypadku t) dla dwóch dowolnych punktów prostej.

W trygonometrii ten stosunek nazywany jest tangensem. Nachylenie krzywej jest równe wartości jej pochodnej. Przyspieszenie zależy od zmiany prędkości w czasie – jest jej pochodną.

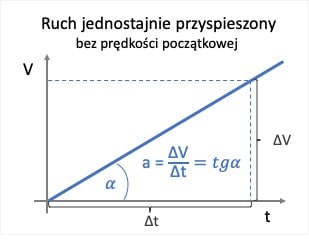
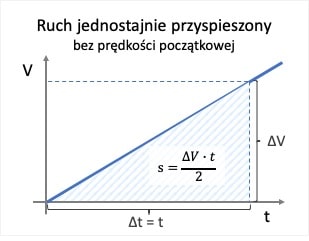
W ruchu jednostajnie przyspieszonym bez prędkości początkowej pole trójkąta pod wykresem zależności prędkości od czasu odpowiada przebytej drodze.

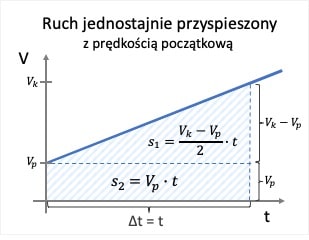
W ruchu jednostajnie przyspieszonym z prędkością początkową na wykresie zależności prędkości od czasu droga będzie sumą pól kwadratu oraz trójkąta.

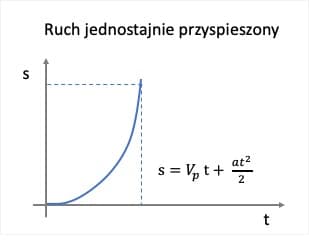
W ruchu jednostajnie przyspieszonym zależność drogi od czasu jest funkcją kwadratowa – jej wykresem jest parabola.

7. Swobodny spadek

Swobodne spadanie to ruch ciała puszczonego z pewnej wysokości np. jabłka spadającego z drzewa. Jeżeli zaniedbamy opory powietrza taki ruch możemy traktować jako ruch jednostajny przyspieszony, spowodowany przez grawitację, ze stałym przyspieszeniem ziemskim g.

Średnia wartość g dla Ziemi wynosi 9,81 m/s². A zatem prędkość spadającego swobodnie ciała rośnie jednostajnie w każdej sekundzie o 9,81 m/s. W swobodnym spadaniu prędkość początkowa ciała jest równa zero. Wartość prędkości możemy wyrazić za pomocą wzoru:

\large V = g \cdot t

V – wartość prędkości
g – wartość przyspieszania
t – czas od momentu rozpoczęcia spadku

Aby obliczyć wysokość, na której znajduje się ciało po upływie czasu t odejmujemy od wysokości początkowej drogę pokonaną przez ciało ruch jednostajnie przyspieszonym z przyspieszeniem ziemskim:

\large h = h_o - \frac{g \cdot t^2}{2}

h – wysokość, na której znajduje się ciało
h₀ – wysokość początkowa, z której zrzucono ciało
g – wartość przyspieszenia
t – czas od momentu rozpoczęcia spadku

Czas spadania możemy wyliczyć ze wzoru na wysokość zauważając, że wysokość h w momencie upadku będzie równa zero.

\large 0 = h_o - \frac{g \cdot t^2}{2} \large \frac{g \cdot t^2}{2} = h_o \large g \cdot t^2 = 2 \cdot h_o \large t^2 = \frac{2 \cdot h_o}{g} \large t = \sqrt{\frac{2 \cdot h_o}{g}}

Wartość prędkości końcowej w chwili upadku policzymy podstawiając wyliczony czas spadania do wzoru na prędkość:

\large V = g \cdot t \large V = g \cdot \sqrt{\frac{2 \cdot h_o}{g}} \large V = \sqrt{\frac{2 \cdot h_o \cdot g^2}{g}} \large V = \sqrt{2 h_o g}

8. Rzut pionowy

Rzut pionowy to ruch w polu grawitacyjnym Ziemi z prędkością początkową skierowaną do góry np. ruch piłki wyrzuconej pionowo w powietrze. W uproszczeniu możemy przyjąć, że wyrzucone do góry ciało porusza się najpierw ruchem jednostajnie opóźnionym z przyspieszeniem ziemskim g a po osiągnięciu najwyższego punktu zaczyna opadać poruszając się ruch jednostajnie przyspieszonym z przyspieszeniem ziemskim g.

Czas wznoszenia w ruchu pionowym, możemy obliczyć z równania ruchu pamiętając, że prędkość końcowa będzie równa zero.

\large V_k = V_p - g \cdot t_w \large 0 + V_p = g \cdot t_w \large t_w = \frac{V_p}{g}

Osiągniętą w rzucie pionowym wysokość maksymalną (czyli przesunięcie) możemy policzyć z równania ruchu jednostajnie opóźnionego, podstawiając wyliczony wcześniej czas wznoszenia.

\large h = V_p \cdot t_w \:- \frac{gt_w^2}{2} \large h = V_p \cdot \frac{V_p}{g} \:- \frac{g{\frac{V_p^2}{g^2}}}{2} \large h = \frac{V_p^2}{g} \:- \frac{V_p^2}{2g} \Large h = \frac{V_p^2}{2g}

W rzucie pionowym czas wznoszenia jest równy czasowi spadania. Dlatego całkowity czas lotu do momentu powrotu ciała na pozycją początkową be∂zie dokładnie dwa razy większy od czasu wznoszenia.

\large t_k = \frac{2V_p}{g}

Zastosowane uproszczenia w modelu rzutu pionowego dotyczą: pominięcia oporów powietrza, efektów ruchu obrotowego ziemi oraz założenie jednorodności pola grawitacyjnego Ziemi.

9. Rzut poziomy

Rzut poziomy to ruch ciała wyrzuconego w kierunku poziomym z pewnej wysokości np. ruch wyrzuconego prosto kamienia kiedy stoimy nad przepaścią lub zrzuconej z samolotu bomby. W uproszczeniu możemy przyjąć, że rzut poziomy składa się z dwóch występujących jednocześnie ruchów: ruchu jednostajnego z prędkością początkową w kierunku poziomym oraz ruchu jednostajnie przyspieszonego (swobodnego spadku) w kierunku pionowym pod wpływem grawitacji.

Zauważmy, że ciało pozostanie w ruchu do momentu upadku (przy kiedy jego wysokość osiągnie 0) a więc dokładnie tak samo jak w swobodnym spadaniu:

\large t = \sqrt{\frac{2 \cdot h_o}{g}}

Zasięg rzutu poziomego możemy obliczyć mnożąc czas ruchu przez prędkość początkową ciała w kierunku poziomym.

\large Z = V_o \cdot t \large Z = V_o \sqrt{\frac{2 \cdot h_o}{g}}

Wartość prędkości w dowolnym momencie ruchu możemy obliczyć z twierdzenia Pitagorasa znając jej składowe poziomą oraz pionową.

\large V = \sqrt{V_x^2 + V_y^2} \large V_x = V_0 \large V_y = g \cdot t \large V = \sqrt{V_0^2 + (gt)^2}

Zastosowane uproszczenia w modelu rzutu poziomego dotyczą: pominięcia oporów powietrza, efektów ruchu obrotowego ziemi oraz założenie jednorodności pola grawitacyjnego Ziemi.

10. Rzut ukośny

Rzut ukośny to ruch ciała wyrzuconego pod pewnym kątem do poziomu z prędkością początkową V₀ np. ruch piłki wykopanej przez bramkarza, ruch oszczepu wyrzuconego przez sportowca czy ruch pocisku wystrzelonego z moździerza. W uproszczeniu możemy przyjąć, że rzut poziomy składa się z dwóch występujących jednocześnie ruchów: ruchu jednostajnego w kierunku poziomym z prędkością V_0x oraz rzutu pionowego z prędkością początkową V_0y pod wpływem grawitacji.

Korzystając z funkcji trygonometrycznych możemy wyrazić początkowe prędkości w kierunkach poziomym i pionowym (składowe prędkości początkowej V₀):

\large V_{oy} = V_0 \cdot sin(\alpha) \large V_{ox} = V_0 \cdot cos(\alpha)

Możemy zauważyć, że rzut pionowy jest szczególnym przypadkiem rzutu ukośnego, w którym kąt rzutu to 90° (sinus 90° jest równy 1).

Wartość prędkości w dowolnym momencie ruchu możemy wyrazić za pomocą jej składowych korzystając z twierdzenia Pitagorasa:

\large V = \sqrt{V_x^2 + V_y^2} \large V_x = V_0 \large V_y = g \cdot t

Wzór na czas wznoszenia będzie analogiczny do wzoru czas wznoszenia przy rzucie pionowym ale tym razem użyjemy składowej pionowej prędkości:

\large t_w = \frac{V_{0y}}{g} \large t_w = \frac{V_0 \cdot sin(\alpha)}{g}

Osiągniętą w rzucie ukośnym wysokość maksymalną (czyli przesunięcie) możemy policzyć z równania ruchu jednostajnie opóźnionego (podobnie jak w rzucie pionowym ale dla składowej pionowej prędkości), podstawiając wyliczony wcześniej czas wznoszenia.

\large h = V_{oy} \cdot t_w \:- \frac{gt_w^2}{2} \large h = V_{oy} \cdot \frac{V_{0y}}{g} \:- \frac{(\frac{V_{0y}}{g})^2}{2} \large h =\frac{V_{0y}}{2g} \large h =\frac{V_0 \cdot sin(\alpha)}{2g}

Całkowity czas ruchu w rzucie ukośnym będzie dokładnie dwa razy większy od czasu wznoszenia (fazy wznoszenia i opadania trwają tyle samo).

\large t_c = \frac{2 V_0 \cdot sin(\alpha)}{g}

Teraz możemy obliczyć zasięg. W ruchu ukośnym ciało porusza się ruchem jednostajnym w kierunku poziomym.

\large Z = V_{0x} \cdot t_c \large Z = V_0 \cdot cos(\alpha) \cdot \frac{2 V_0 \cdot sin(\alpha)}{g} \large Z = \frac{V_0^2}{g} \cdot 2 sin(\alpha) cos (\alpha) \large Z = \frac{V_0^2}{g} \cdot sin(2\alpha)

Pod jakim kątem rzucić kamień aby doleciał jak najdalej? Maksymalna wartość funkcji sinus to 1, sin(2α) = 1 dla α = 45°.

Jeżeli zaniedbamy opory powietrza torem ciała w rzucie ukośnym będzie parabola. W rzeczywistości opór powietrza będzie spowalniał ciało i jego zasięg będzie nieco mniejszy. Torem ciała w uwzględnieniem oporu powietrza będzie tzw. krzywa balistyczna – przypominająca parabolę ale “opadająca” coraz szybciej w czasie.

Zastosowane uproszczenia w modelu rzutu ukośnego dotyczą: pominięcia oporów powietrza, efektów ruchu obrotowego ziemi oraz założenie jednorodności pola grawitacyjnego Ziemi.

11. Ruch jednostajny po okręgu

Ruch jednostajny po okręgu jest szczególnym przypadkiem ruchu krzywoliniowego, w którym torem ciała jest okrąg a wartość prędkości nie zmienia się. Przykładami ruchu jednostajnego po okręgu są: ruch księżyca wokół Ziemi, ruch dziecka na karuzeli, ruch płyty CD czy też śmigła samolotu.

11.1. Okres ruchu po okręgu

Czas, w ciągu którego ciało wykona pełny obrót czyli wróci do punktu wyjścia nazywamy okresem ruchu T. Przykładowo, jeżeli satelita okrąża Ziemię w ciągu 24h to okresem jego ruchu jest właśnie 24 h (czyli 24 x 60 x 60 s = 86 400 s). Okres ruchu możemy obliczyć dzieląc czas ruchu przez liczbę okrążeń (obrotów):

\large T = \frac{t}{N}

T – okres ruchu
t – czas ruchu
N – liczba wykonanych obrotów

11.2. Częstotliwość w ruchu po okręgu

Opisując ruch po okręgu często zamiast okresu ruchu posługujemy się pojęciem jego częstotliwości np. dysk twardy wykonuje 7200 obrotów na minutę, płyta gramofonowa wykonuje 33,3 obroty na minutę, bęben pralki wykonuje 1200 obrotów na minutę, wał silnika samochodu elektrycznego wykonuje nawet 300 obrotów na sekundę. Częstotliwość f jest odwrotnością okresu czyli możemy ją obliczyć dzieląc liczbę obrotów przez czas:

\large f = \frac{1}{T} = \frac{N}{t}

Jednostką częstotliwości jest 1/s czyli 1 Hz (herc).

11.3. Prędkość Liniowa

Wartość prędkości liniowej w ruchu jednostajnym po okręgu możemy obliczyć dzieląc drogę czyli obwód koła (2πr) przez czas potrzebny na pokonanie tej drogi czyli okres ruchu T. Alternatywnie możemy drogę pomnożyć przez odwrotność okresu czyli częstotliwość f.

\large V = \frac{2 \pi r}{T} = 2 \pi r f

W ruchu jednostajnym po okręgu wartość prędkości liniowej nie zmienia się czyli przyspieszenie, odpowiadające za zmianę prędkości (zwane przyspieszeniem stycznym) jest równe zero.

11.4. Przyspieszenie dośrodkowe

Wartość prędkości liniowej w ruchu jednostajnym po okręgu nie zmienia się. Ale czy to oznacza, że prędkość jest stała? Nie, w ruchu po okręgu. Prędkość liniowa jest wektorem i oprócz wartości posiada jeszcze kierunek. Kierunek ten zmienia się cały czas zakrzywiając tor ruchu. Gdyby się nie zmieniał to ciało zamiast poruszać się po okręgu zostałoby wystrzelone w lini prostej. Skoro prędkość liniowa zmienia się to oznacza, że mamy też do czynienia z przyspieszeniem. Zmianę kierunku ruchu w ruchu krzywoliniowym takim jak ruch po okręgu pokazuje nam przyspieszenie dośrodkowe:

\large a_d = \frac{V^2}{R}

11.5. Prędkość kątowa

Prędkość liniowa pomaga nam wyrazić jak szybko i w którym kierunku (jest wektorem) ciało przemiesza się w czasie. Aby wyrazić jak szybko ciało obraca się używamy prędkości kątowej. Wartość prędkości kątowej obliczamy dzieląc kąt zakreślony przez ciało (zwany przemieszczeniem kątowym lub drogą kątową) przez czas zakreślenia.

\large \omega = \frac{\Delta \alpha}{\Delta t}

11.6. Przyspieszenie kątowe

Zmianę prędkości kątowej w czasie opisuje przyspieszenie kątowe. Przyspieszenie kątowe zależy od zmian prędkość – jest jego pochodną.

\large \epsilon = \frac{\Delta \omega}{\Delta t}

11.7. Zależność pomiędzy prędkością liniową a kątową

Jaka jest zależność pomiędzy prędkością liniową a kątowa? Zauważmy, że prędkość w ruchy jednostajnym to:

\large V = \frac{\Delta s}{\Delta t}

W ruchu po okręgu drogą będzie długość pokonanego łuku, która możemy obliczyć mnożąc promień przez zakreślony kąt.

\large s = l = r \cdot \Delta \alpha

Podstawiając do wzoru na prędkość liniową:

\large V = \frac{\Delta s}{\Delta t} = \frac{r \cdot \Delta \alpha}{\Delta t}

I wykorzystując definicję prędkości kątowej:

\large V = r \cdot \omega