Prawo Pascala

Wyciskając pastę do zębów z tubki, nadmuchując balonik czy podnosząc samochód na podnośniku w warsztacie – korzystamy z prawa Pascala.

Prawo Pascala głosi, że ciśnienie zewnętrzne wywierane na gaz lub ciecz rozchodzi się we wszystkich kierunkach jednakowo. W praktyce, prawo to pozwala zwielokrotnić siłę nacisku i jest wykorzystywane w konstrukcji podnośników, pras, układów hamulcowych oraz pomp.

1. Definicja

Prawo Pascala: Zmiana ciśnienia w zamkniętym płynie (gazie lub cieczy) jest przenoszona bez zmiany wartości do każdego miejsca w płynie i do ścian zbiornika.

Prawo Pascala zostało opublikowane przez francuskiego matematyka Blaise’a Pascala w 1653 roku.

2. Zastosowanie

Jednym z popularnych zastosowań prawa Pascala jest podnośnik hydrauliczny, który pozwala zwielokrotnić zastosowaną siłę do podnoszenia masywnych obiektów, na przykład samochodów w warsztatach.

Podnośnik jest urządzeniem wypełnionym nieściśliwą cieczą (zwykle olejem), które składa się z dwóch tłoków: mniejszego – roboczego oraz większego – pompy.

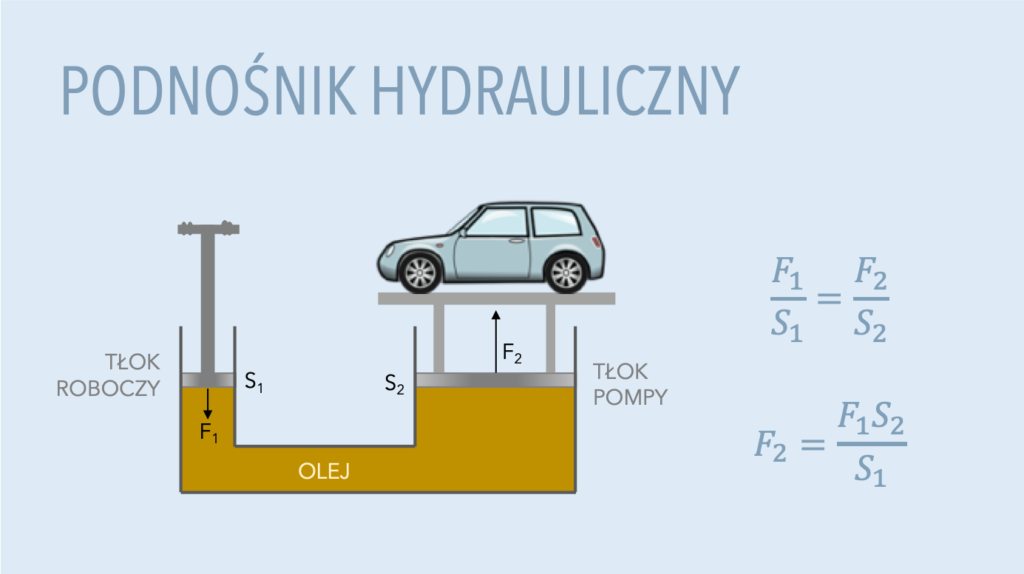
Ponieważ, zgodnie z prawem Pascala ciśnienie wywierane na tłok roboczy będzie równe ciśnieniu działającego na tłok pompy:

p_1 = p_2

Możemy zastosować wzór na ciśnienie p = F / S:

\frac{F_1}{S_1} = \frac{F_2}{S_2}

Przekształcając, wyliczamy siłę tłoka pompy. Ponieważ pole powierzchni tłoka pompy S2 jest większe od pola powierzchni tłoka roboczego S1 to siła tłoka pompy będzie większa niż siła, która trzeba użyć do przesunięcia tłoka roboczego.

F_2 = \frac{F_1S_2}{S_1}

Gdzie F1 – siła parcia na tłok roboczy, F2 – siła działająca na tłok pompy, S1 – powierzchnia tłoka roboczego, S2 – powierzchnia tłoka pompy.

3. Inne zastosowania prawa Pascala

  • dmuchanie balonów
  • pompowanie dmuchanego materaca
  • prasa hydrauliczna,
  • pompa hydrauliczna
  • układ hamulcowy

4. Zadanie

Z jaką najmniejszą siła F1 należy działać na tłok roboczy podnośnika hydraulicznego o średnicy 2 cm aby unieść zabytkowy samochód Polski Fiat 125p o masie 970 kg na tłoku pompy o średnicy 24 cm?

F1 = ?

Korzystając ze wzoru na pole koła S = πr2 i pamiętając, że promień koła jest równy połowie długości jego średnicy r=d/2 możemy zapisać równania powierzchni tłoków:

S1 = π(d1/2)2

S2 = π(d2/2)2

Siła tłoka pompy będzie musiała zrównoważyć siłę grawitacji:

F2 = mg

Zgodnie z prawem Pascala ciśnienie wywierane na tłok roboczy będzie równe ciśnieniu działającego na tłok pompy:

p1= p2

I stosując wzór na ciśnienie p = F / S:

\frac{F_1}{S_1} = \frac{F_2}{S_2}

Wyliczamy siłę tłoka roboczego.

F_1 = \frac{F_2S_1}{S_2}

Podstawiamy wcześniej wyprowadzone wzory na siłę tłoka pompy i powierzchnie tłoków:

F_1 = \frac{mg \cdot \pi (\frac{d1}{2})^2}{\pi (\frac{d2}{2})^2}

Skracamy π/4 (2 z mianownika podniesioną do kwadratu).

F_1 = \frac{mg \cdot d_1^2}{d_2^2}

I podstawiamy, skracając centymetry kwadratowe (co pozwala ominąć zamianę jednostek na metry):

F_1 = \frac{970 kg \cdot 10 m/s^2 \cdot 4}{576}

F1 = ~67 N

PRZYDATNY ARTYKUŁ?
Udostępnij link innym:

Facebooktwitterpinterestmail

Dodaj do Google Classroom

Następny temat:
Ciśnienie hydrostatyczne

Pozostałe tematy z działu właściwości materii:

Masa i ciężar | Stany skupienia | Gęstość | Parcie i ciśnienie | Ciśnienie atmosferyczne | Prawo Pascala | Ciśnienie hydrostatyczne | Siła wyporu i prawo Archimedesa | Napięcie powierzchniowe