W tym artykule znajdziesz najważniejsze informacje o prawie Archimedesa, sile wyporu a także dowiesz się z niego jaki jest wzór na siłę wyporu i poznasz warunek pływania ciał. Na końcu artykułu znajdziesz zadania z rozwiązaniami.

Prawo Archimedesa
Siła wyporu
Wzór na siłę wyporu
Warunek pływania ciał

Przykładowe zadania:

Zadanie 1: siła wyporu działająca na nurka
Zadanie 2: drewniany klocek zanurzony do 3/4 objętości
Zadanie 3: pływająca tafla lodu z niedźwiedziem polarnym

1. Prawo Archimedesa

Prawo Archimedesa: Na ciało zanurzone w cieczy działa siła wyporu, skierowana ku górze i równa co do wartości ciężarowi cieczy wypartej przez to ciało.

Prawo Archimedesa zostało sformułowane już w starożytności przez greckiego uczonego Archimedesa z Syrakuz.

Prawo Archimedesa niekiedy jest zapisywane w postaci alternatywnej: Ciało zanurzone w cieczy traci pozornie na ciężarze tyle, ile waży ciecz wyparta przez to ciało.

Ciężar wypartej cieczy = ciężar ciała – ciężar ciała w wodzie lub
Ciężar ciała w wodzie = ciężar ciała – ciężar wypartej cieczy

Zależność ta ma także zastosowanie do gazów.

Kiedy prawo Archimedesa nie jest spełnione?

Prawo Archimedesa nie uwzględnia napięcia powierzchniowego cieczy. Prawo Archimedesa nie jest spełnione w cieczach złożonych (zawierających mieszanki stanów np. stały-ciekły, ciekły-gazowy).

2. Siła wyporu

Siła wyporu to siła działająca na ciało zanurzone w cieczy (oraz gazie). Jest to siła przeciwna to siły ciężkości. Siłą wyporu musi być równa sile ciężkości pływającego ciała.

Siła wyporu zależy od gęstości cieczy oraz objętości zanurzonej części ciała.

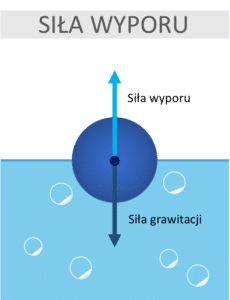
Przykłady siły wyporu:

drewniana belka wrzucona do wody wypłynie na powierzchnie (drewno ma mniejszą gęstość od wody)
lód jest lżejszy od wody (ma mniejsza gęstość), więc unosi się na jej powierzchni
statki pływają po powierzchni wody gdyż siła wyporu równoważy siłę ciężkości
balony oraz sterowce unoszą się w powietrzu ponieważ wypełnione są gazami lżejszymi (o mniejszej gęstości) od powietrza

Ciekawostka

Statek wypływając z Wisły na Morze Bałtyckie zmniejszy swoje zanurzenie gdyż słona woda morska ma większą gęstość. Jak to możliwe?

Siła wyporu musi być równa sile ciężkości a ciężar statku się nie zmieni. Zmiana gęstość wody zostanie zrekompensowana przez zmianę zanurzenia a dokładniej objętości zanurzonej części ciała. Skoro gęstość się zwiększy to (proporcjonalnie) objętość zanurzenia się zmniejszy. )

3. Wzór na siłę wyporu

Siłę wyporu możemy zapisać wzorem:

F_w = \rho \cdot g \cdot V

Gdzie: Fw – siła wyporu, ρ – gęstość cieczy, g – przyspieszenie ziemskie, V – objętość zanurzonej części ciała (oraz wypartej cieczy)

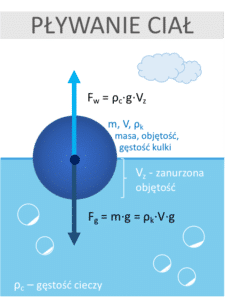
Interpretacja prawa Archimedesa: Na każde ciało zanurzone w cieczy działa siła wyporu. Zanurzenie ciała spowoduje wyparcie cieczy (lub podniesienie jej poziomu). Objętość wypartej cieczy jest taka sama jak objętość zanurzonego ciała.

4. Warunek pływania ciał

Siła wyporu musi być równa sile ciężkości pływającego ciała.

Jeśli gęstość ciała jest większa od gęstości cieczy, ciało tonie.
Jeśli gęstość ciała jest mniejsza niż gęstość cieczy, ciało wypływa na powierzchnię.
Jeśli gęstość ciała jest równa gęstości cieczy, ciało pływa (tkwi) całkowicie zanurzone pod powierzchnią cieczy.

5. Przykładowe zadania

Przykładowe zadanie 1: siła wyporu działająca na nurka

Pasjonaci nurkowania chwalą sobie Morze Bałtyckie między innymi ze względu na łatwość zanurzania. Policz siłę wyporu działająca na nurka o objętości V= 0,06 m3, przyjmując g=10 m/s2 w

a) Morzu Bałtyckim, gdzie gęstość wody wynosi ρ = 1003 kg/m3
b) Morzu Czerwonym, gdzie gęstość wody wynosi ρ = 1025 kg/m3

Rozwiązanie:

Nurek jest w całości zanurzony w wodzie. Z wzoru na siłę wyporu Fw = ρ ⋅ g ⋅ V

a) Siła wyporu w Morzu Bałtyckim Fw = 1003 kg/m3 ⋅ 10 m/s2 ⋅ 0,06 m3 = 601,8 N
b) Siła wyporu w Morzu Czerwonym Fw = 1025 kg/m3 ⋅ 10 m/s2 ⋅ 0,06 m3 = 615 N

Przykładowe zadanie 2: drewniany klocek zanurzony do 3/4 objętości

Drewniany klocek pływa po wodzie zanurzony do 3/4 swojej objętości. Jaka jest gęstość drewna z którego wykonano klocek? Gęstość wody wynosi ρ=1000 kg/m3.

Rozwiązanie:

Z pierwszej zasady dynamiki – siła grawitacji jest równa sile wyporu działającej na 3/4 objętości klocka.

F_w = F_g

ρ_w ⋅ g ⋅ 3/4 V = m ⋅ g

Masa ciała to m = ρ_c ⋅ V a zatem

ρ_w ⋅ g ⋅ 3/4 V = ρc ⋅ V ⋅ g, skracając V oraz g

3/4 ρ_w = ρ_c i podstawiając

ρ_c = 3/4 ⋅ 1000 kg/m³ = 750 kg/m³

Przykładowe zadanie 3: pływająca tafla lodu z niedźwiedziem polarnym

Jak duża powinna być tafla lodu o grubości d = 0,3 m aby utrzymała na wodzie ciężar niedźwiedzia polarnego o masie 500 kg? Gęstość lodu wynosi ρk = 917 kg/m³ a gęstość wody to ρw =1027 kg/m³..

Rozwiązanie:

Aby kra lodowa wraz z niedźwiedziem nie zatonęła siła wyporu musi zrównoważyć siłę ciężkości.

F_w = F_g

Korzystając ze wzorów na siłę wyporu działającą na krę (F_w = ρ ⋅ g ⋅ V) oraz siłę grawitacji działającą na krę i niedźwiedzia (F_g = m ⋅ g):

ρ_w \cdot g \cdot V_{kry} = (m_{kry} + m_{niedźwiedzia}) \cdot g

Skracamy g. Masa ciała to m = ρ ⋅ V a zatem rozpisując masę kry:

ρ_w \cdot V_{kry} = ρ_{kry} ⋅ V_{kry} + m_{niedzwiedzia}

Dzielimy przez V_kry i przenosimy ρ_kry

ρ_w - ρ_{kry} =⋅ \frac{m_{niedzwiedzia}}{V_{kry}}

\frac{1}{V_{kry}} = \frac{ρ_w - ρ_{kry}}{m_{niedźwiedzia}}

V_{kry} = \frac{m_{niedźwiedzia}}{ρ_w - ρ_{kry}}

ponieważ objętość obliczamy mnożąc powierzchnię S przez wysokość d

V_{kry} = S \cdot d

podstawiając objętość do wzoru na powierzchnię:

S = \frac{m_{niedźwiedzia}}{d(ρ_{w} - ρ_{kry})}

Podstawiając wartości:

S = \frac{500 kg}{0,3 m (1027 \frac{kg}{m^3}- 917 \frac{kg}{m^3})}

S = ~15m²

PRZYDATNY ARTYKUŁ?
Udostępnij link innym:

Dodaj do Google Classroom

Następny temat:
Napięcie powierzchniowe