W tym artykule znajdziesz najważniejsze informacje o ruchu jednostajnym prostoliniowym – dowiesz się czym jest ruch jednostajny prostoliniowy oraz poznasz wzory na prędkość i drogę w tym ruchu.
1. Ruch jednostajny prostoliniowy
Ruch jednostajny prostoliniowy to taki ruch, którego torem jest linia prosta a prędkość ciała jest stała np. ruch pociągu lub samochodu poruszających się ze stałą prędkością po lini prostej.
W ruchu jednostajnym prostoliniowym ciało w jednakowych odcinkach czasu przebywa jednakową drogę. Droga ta jest proporcjonalna do czasu trwania ruchu.
Przykład: Jeżeli samochód porusza się ruchem jednostajnym prostoliniowym z prędkością 10 m/s to w czasie 1 sekundy pokona 10 metrów, w ciągu 2 sekund 20 metrów i tak dalej.
2. Prędkość w ruchu jednostajnym prostoliniowym
W ruchu prostoliniowym, zwrot prędkości nie zmienia się a długość wektora przesunięcia jest równa przebytej drodze. Wartość prędkości (szybkość) V można wtedy obliczyć dzieląc drogę s przez czas t, w którym ta droga została przebyta.
Jednostką prędkości jest 1 m/s. Ciało porusza się z prędkością 1 m/s, jeżeli drogę 1 metra przebędzie w ciągu 1 sekundy.
Wykres prędkości od czasu w ruchu jednostajnym prostoliniowym
Ponieważ prędkość w ruchu jednostajnym, prostoliniowym nie zmienia się, wykresem zależności prędkości od czasu dla ruchu jednostajnego jest prosta równoległa do osi czasu.
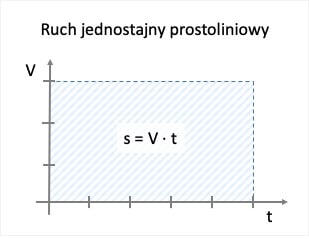
Wyliczając ze wzoru na prędkość drogę otrzymujemy s = V ⋅ t. Tym samym wzorem możemy wyrazić pole prostokąta pod wykresem zależności prędkości od czasu – pole to odpowiada przebytej drodze.
3. Droga w ruchu jednostajnym prostoliniowym
W ruchu jednostajnym prostoliniowym ciało w jednakowych odcinkach czasu przebywa jednakową drogę. Droga ta jest proporcjonalna do czasu trwania ruchu.
Wykres drogi od czasu w ruchu jednostajnym prostoliniowym
Wykres zależności drogi od czasu dla ruchu jednostajnego prostoliniowego to linia prosta o nachyleniu odpowiadającym prędkości ciała będącego w ruchu. Im większa prędkość ciała tym większe będzie nachylenie prostej (bardziej stroma będzie prosta).
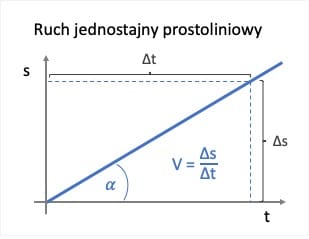
Zauważmy, że wykres ten przedstawia funkcję liniową: s = V ⋅ t. Dla funkcji liniowej nachylenie jest określone przez współczynnik kierunkowy prostej – w tym przypadku V.
Nachylenie prostej czyli prędkość możemy opisać matematycznie jako stosunek zmiany wartości na osi Y (w tym przypadku s) to zmiany wartości na osi X ( w tym przypadku t) dla dwóch dowolnych punktów prostej.
\Large V = \frac{\Delta s}{\Delta t} W trygonometrii ten stosunek nazywany jest tangensem. Prędkość zależy od zmiany drogi w czasie – czyli jest jego pochodną. Nachylenie krzywej (tangens) jest równe wartości jej pochodnej.
PRZYDATNY ARTYKUŁ? Udostępnij link innym:

Następny temat:
Ruch jednostajnie przyspieszony
Pozostałe tematy z działu: Kinematyka
Układ odniesienia | Względność ruchu | Tor | Droga | Jednostka czasu: sekunda | Prędkość | Przyspieszenie | Ruch jednostajny prostoliniowy | Ruch jednostajnie przyspieszony (opóźniony) | Swobodny spadek



