W tym artykule znajdziesz najważniejsze wzory matematyczne na objętość (np. walca, kuli oraz wiele innych) oraz informacje o objętości ciał w fizyce i chemii:
- Wzór na objętość – fizyka
- Wzór na objętość – chemia
- Wzór na objętość sześcianu
- Wzór na objętość walca
- Wzór na objętość kuli
- Wzór na objętość prostopadłościanu
- Wzór na objętość graniastosłupa
- Wzór na objętość stożka
- Wzór na objętość ostrosłupa
Wzór na objętość – fizyka
W fizyce, wzór na objętość możemy wyprowadzić ze wzoru na gęstość. Ponieważ gęstość substancji obliczamy dzieląc masę ciała przez jego objętość to przekształcając:
Objętość możemy obliczyć dzieląc masę ciała przez jego gęstość
\Large V = \frac{m}{\rho} V – objętość ciała
m – masa ciała
\rho – gęstość ciała oznaczana jako rho (czytaj ro)
Wzór na objętość – chemia
W chemii, do obliczenia objętości zastosujemy dokładnie ten sam wzór co w fizyce ale zwyczajowo oznaczymy gęstość jako d a nie \rho (rho).
\Large V = \frac{m}{d} V – objętość ciała
m – masa ciała
d – gęstość ciała oznaczana w chemii jako d (zamiast rho)
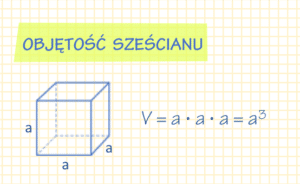
Wzór na objętość sześcianu
Objętość sześcianu możemy obliczyć mnożąc przez siebie jego wymiary: głębokość, szerokość i wysokość. W przypadku sześcianu są one równe.
\Large V = a \cdot a \cdot a = a^3 V – objętość sześcianu
a – długości ściany sześcianu
Wzór na objętość walca
Objętość walca możemy obliczyć mnożąc przez siebie pole jego podstawy (czyli pole koła) przez wysokość. Dla przypomnienia pole koła opisuje wzór \pi \cdot r^2 .
V = \pi r^2 \cdot h V – objętość walca
r – promień podstawy walca
h – wysokość walca
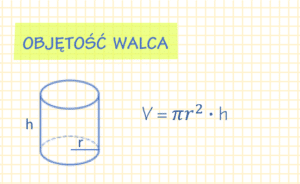
Wzór na objętość kuli
Objętość kuli możemy obliczyć za pomocą wzoru:
V = \frac{4}{3} \pi r^3 V – objętość kuli
r – promień kuli

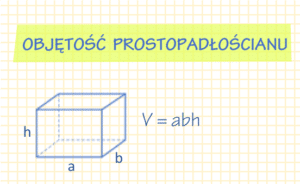
Wzór na objętość prostopadłościanu
Objętość prostopadłościanu możemy obliczyć mnożąc przez siebie jego wymiary: głębokość, szerokość i wysokość.
V = a \cdot b \cdot h V – objętość prostopadłościanu
a – szerokość prostopadłościanu
b – głębokość prostopadłościanu
h – wysokość prostopadłościanu
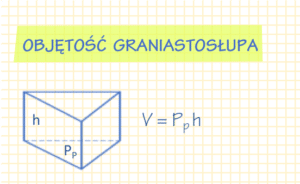
Wzór na objętość graniastosłupa
Objętość graniastosłupa możemy obliczyć mnożąc przez siebie pole jego podstawy przez wysokość.
V = P_p \cdot h V – objętość graniastosłupa
P_p – pole podstawy graniastosłupa
h – wysokość graniastosłupa
Wzór na objętość stożka
Objętość stożka możemy obliczyć za pomocą wzoru:
V = \frac{1}{3} \pi r^2 h V – objętość stożka
r – promień postawy stożka
h – wysokość stożka
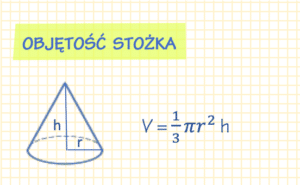
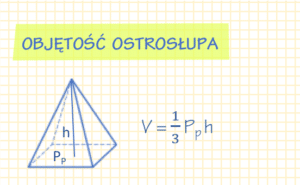
Wzór na objętość ostrosłupa
Objętość ostrosłupa możemy obliczyć za pomocą wzoru:
V = \frac{1}{3} P_p h V – objętość ostrosłupa
P_p – pole podstawy ostrosłupa
h – wysokość ostrosłupa
A może szukasz innych wzorów i definicji z fizyki? Koniecznie zajrzyj do mojej listy wzorów i zagadnień!
