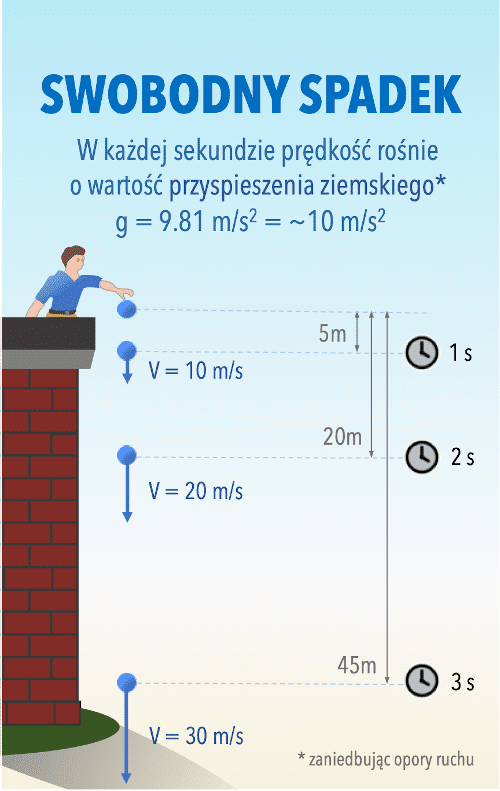
Swobodny spadek to ruch ciała puszczonego z pewnej wysokości np. jabłka spadającego z drzewa. Jeżeli zaniedbamy opory powietrza to swobodne spadanie możemy traktować jako ruch jednostajny przyspieszony ze stałym przyspieszeniem ziemskim g, spowodowany przez grawitację.
1. Przyspieszenie
Z jakiem przyspieszeniem poruszają się swobodnie spadające ciała? Średnia wartość przyspieszenia ziemskiego g wynosi 9,81 m/s2. To oznacza, że prędkość spadającego swobodnie ciała rośnie jednostajnie w każdej sekundzie o 9,81 m/s (jeżeli zaniedbamy opory ruchu).
W swobodnym spadaniu prędkość początkowa ciała jest równa zero.
2. Prędkość
Wartość prędkości podczas swobodnego spadku możemy wyrazić za pomocą wzoru:
V = g \cdot t
V – wartość prędkości
g – wartość przyspieszania
t – czas od momentu rozpoczęcia spadku
3. Wysokość
Aby obliczyć wysokość, na której znajduje się ciało po upływie czasu t odejmujemy od wysokości początkowej drogę pokonaną przez ciało ruch jednostajnie przyspieszonym z przyspieszeniem ziemskim:
h = h_o – \frac{g \cdot t^2}{2}h – wysokość, na której znajduje się ciało po upływie czasu t
h0 – wysokość początkowa, z której zrzucono ciało
g – wartość przyspieszenia
t – czas od momentu rozpoczęcia spadku
4. Czas spadania
Czas spadania możemy wyliczyć ze wzoru na wysokość zauważając, że wysokość h w momencie upadku będzie równa zero.
0 = h_o – \frac{g \cdot t^2}{2}\frac{g \cdot t^2}{2} = h_og \cdot t^2 = 2 \cdot h_o
\frac{g \cdot t^2}{2} = h_og \cdot t^2 = 2 \cdot h_o
t^2 = \frac{2 \cdot h_o}{g}t = \sqrt{\frac{2 \cdot h_o}{g}}Wartość prędkości końcowej w chwili upadku policzymy podstawiając wyliczony czas spadania do wzoru na prędkość:
V = g \cdot t
V = g \cdot \sqrt{\frac{2 \cdot h_o}{g}}V = \sqrt{\frac{2 \cdot h_o \cdot g^2}{g}}V = \sqrt{2 h_o g}PRZYDATNY ARTYKUŁ? Udostępnij link innym:

Poprzedni temat:
Ruch jednostajnie przyspieszony
Pozostałe tematy z działu: Kinematyka
Układ odniesienia | Względność ruchu | Tor | Droga | Jednostka czasu: sekunda | Prędkość | Przyspieszenie | Ruch jednostajny prostoliniowy | Ruch jednostajnie przyspieszony (opóźniony) | Swobodny spadek